LA LUZ

La luz emitida por las fuentes luminosas es capaz de viajar a través de materia o en ausencia de ella, aunque no todos los medios permiten que la luz se propague a su través.

Desde este punto de vista, las diferentes sustancias materiales se pueden clasificar en opacas, transparentes y traslucidas.Aunque la luz es incapaz de traspasar las opacas, puede atravesar las otras. Las sustancias transparentes tienen, además, la propiedad de que la luz sigue en su interior una sola dirección. Éste es el caso del agua, el vidrio o el aire. En cambio, en las traslucidas la luz se dispersa, lo que da lugar a que a través de ellas no se puedan ver las imágenes con nitidez. El papel vegetal o el cristal esmerilado constituyen algunos ejemplos de objetos traslúcidos.

Los rayos luminosos representan las direcciones en los que la luz se propaga. Un conjunto de rayos constituye un haz. La luz se propaga en línea recta en un medio transparente y homogéneo.

En un medio que además de ser transparente sea homogéneo, es decir, que mantenga propiedades idénticas en cualquier punto del mismo, la luz se propaga en línea recta. Esta característica, conocida desde la antigüedad, constituye una ley fundamental de la óptica geométrica. Dado que la luz se propaga en línea recta, para estudiar los fenómenos ópticos de forma sencilla, se acude a algunas simplificaciones útiles. Así, las fuentes luminosas se consideran puntuales, esto es, como si estuvieran concentradas en un punto, del cual emergen rayos de luz o líneas rectas que representan las direcciones de propagación.

Un conjunto de rayos que parten de una misma fuente se denomina haz. Cuando la fuente se encuentra muy alejada del punto de observación, a efectos prácticos, los haces se consideran formados por rayos paralelos. Si por el contrario la fuente está próxima la forma del haz es cónica.

La velocidad con que la luz se propaga a través de un medio homogéneo y transparente es una constante característica de dicho medio, y por tanto, cambia de un medio a otro. En la antigüedad se pensaba que su valor era infinito, lo que explicaba su propagación instantánea.

Debido a su enorme magnitud la medida de la velocidad de la luz c ha requerido la invención de procedimientos ingeniosos que superarán el inconveniente que suponen las cortas distancias terrestres en relación con tan extraordinaria rapidez. Métodos astronómicos y métodos terrestres han ido dando resultados cada vez más próximos. En la actualidad se acepta para la velocidad de la luz en el vacío el valor c = 300 000 km/s. En cualquier medio material transparente la luz se propaga con una velocidad que es siempre inferior a c. Así, por ejemplo, en el agua lo hace a 225 000 km/s y en el vidrio a 195 000 km/s.

En óptica se suele comparar la velocidad de la luz en un medio transparente con la velocidad de la luz en el vacío, mediante el llamado índice de refracción absoluto n del medio: se define como el cociente entre la velocidad c de la luz en el vacío y la velocidad v de la luz en el medio, es decir:

Dado que c es siempre mayor que v, n resulta siempre mayor o igual que la unidad. Conforme se deduce de la propia definición cuanto mayor sea el índice de refracción absoluto de una sustancia tanto más lentamente viajará la luz por su interior.

Si lo que se pretende es comparar las velocidades v1 y v2 de dos medios diferentes se define entonces el índice de refracción relativo del medio 1 respecto del 2 como cociente entre ambas:           

o en términos de índices de refracción absolutos,

Un índice de refracción relativo n12 menor que 1 indica que en el segundo medio la luz se mueve más rápidamente que en el primero.

 

LA PRIMERA DETERMINACIÓN EXPERIMENTAL DE LA VELOCIDAD DE LA LUZ

Se denomina refracción luminosa al cambio que experimenta la dirección de propagación de la luz cuando atraviesa oblicuamente la superficie de separación de dos medios transparentes de distinta naturaleza. Las lentes, las máquinas fotográficas, el ojo humano y, en general, la mayor parte de los instrumentos ópticos basan su funcionamiento en este fenómeno óptico.

El fenómeno de la refracción va, en general, acompañado de una reflexión, más o menos débil, producida en la superficie que limita los dos medios transparentes. El haz, al llegar a esa superficie límite, en parte se refleja y en parte se refracta, lo cual implica que los haces reflejado y refractado tendrán menos intensidad luminosa que el rayo incidente. Dicho reparto de intensidad se produce en una proporción que depende de las características de los medios en contacto y del ángulo de incidencia respecto de la superficie límite. A pesar de esta circunstancia, es posible fijar la atención únicamente en el fenómeno de la refracción para analizar sus características.

Cuando un haz de luz alcanza la superficie límite de dos medios transparentes, sufre una refracción en el segundo medio una reflexión en la superficie.

LAS LEYES DE REFRACCIÓN

Recordando que índice de refracción y velocidad son inversamente proporcionales la segunda ley de la refracción se puede escribir en función de los índices de refracción en la forma

o en otros términos:

n1 · sen e1 = n2 · sen e2 = cte
 

Esto indica que el producto del seno del ángulo e por el índice de refracción del medio correspondiente es una cantidad constante y, por tanto, los valores de n y sen e para un mismo medio son inversamente proporcionales.

Debido a que la función trigonométrica seno es creciente para ángulos menores de 90º, de la última ecuación se deduce que si el índice de refracción ni del primer medio es mayor que el del segundo n2, el ángulo de refracción e2 es mayor que el de incidencia e1 y, por tanto, el rayo refractado se aleja de la normal.

Por el contrario, si el índice de refracción n1 del primer medio es menor que el del segundo n2, el ángulo de refracción e2 es menor que el de incidencia el y el rayo refractado se acerca a la normal.

Estas reglas prácticas que se deducen de la ecuación son de mucha utilidad en la representación de la marcha de los rayos, operación imprescindible en el estudio de cualquier fenómeno óptico desde la perspectiva de la óptica geométrica.

La refringencia de un medio transparente viene medida por su índice de refracción. Los medios más refringentes son aquellos en los que la luz se propaga a menor velocidad; se dice también que tienen una mayordensidad óptica. Por regla general, la refringencia de un medio va ligada a su densidad de materia, pues la luz encontrará más dificultades para propagarse cuanta mayor cantidad de materia haya de atravesar para una misma distancia. Así pues, a mayor densidad, menor velocidad y mayor índice de refracción o grado de refringencia.

 

El fenómeno de la refracción luminosa puede ser explicado admitiendo la naturaleza ondulatoria de la luz a partir del principio de Huygens y siguiendo un método geométrico de construcción ideado por él. La noción de rayo en la óptica ondulatoria equivale a la de una línea recta que define la dirección en la que la perturbación progresa a través del medio, siendo perpendicular a los frentes de onda. En las ondas circulares o esféricas los rayos son, pues, radiales.

Sean v1 y v2 las velocidades con las que la luz se propaga en los medios transparentes 1 y 2 y S la superficie límite correspondiente. El frente de ondasupuesto plano se dirige hacia S con una inclinación dada; cuando el borde A alcanza S se convierte, según el principio de Huygens, en un foco emisor de ondas secundarias que se propagan en el segundo medio a una velocidad v2.

Lo mismo sucede con el resto de los puntos del frentecuando alcanza la superficie S; pero debido a que la llegada de cada punto del frentese produce con un cierto retraso respecto de la del anterior, cuando el extremoB llega al punto D, los radios de los frentes de onda secundarios generados serán de diferente tamaño, siendo el radio tanto mayor cuanto más cercano esté el foco secundario al punto A. Trazando la envolvente de todos los frentes de ondas secundarios resultantes se obtiene el nuevo frente.

Dado que el tiempo t que tarda A en llegar a C es el mismo que el que tardaB en llegar a D, es posible escribir la relación:

O lo que es lo mismo:

Del diagrama de rayos resultante se deduce que el ángulo de incidencia e1 coincide con ely el de refraccióncon el, además:

de donde se sigue que:

pero  coincide con el cociente de las velocidades , luego combinando ambas relaciones se tiene finalmente: 

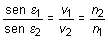
que constituye la ley de Snell de la refracción.

 

-Cálculo de la velocidad de la luz en un medio

Un haz luminoso incide sobre la superficie de un medio cristalino en contacto con el aire formando un ángulo de 30º con la normal a la superficie. Si el ángulo de refracción resultante es de 22º , ¿cuál es la velocidad de la luz en ese medio? (velocidad de la luz en el vacío c = 3 · 10⁸m/s).

De acuerdo con la ley de Snell:

n1 · sen e1 = n2 · sen e2

o en función de las velocidades:

En este caso el medio 1 es el aire y, por tanto, v1 c, de modo que

-Ángulo límite y reflexión total

Cuando un haz luminoso alcanza la superficie de separación de dos medios transparentes, en parte refracta y en parte se refleja. Si el sentido de la propagación es del medio más refringente al medio menos refringente, el rayo refractado, de acuerdo con la ley de Snell, se alejará de la normal.

Eso implica que si se aumenta progresivamente el ángulo de incidencia, el rayo refractado se desviará cada vez más de la normal, aproximándose a la superficie límite hasta coincidir con ella. El valor del ángulo de incidencia que da lugar a este tipo de refracción recibe el nombre de ángulo límite eL.

La determinación del ángulo límite eL puede hacerse a partir de la ley de Snell. Dado que el ángulo de refracción que corresponde al ángulo límite vale 90º, se tendrá:

n1 sen eL = n2 sen 90º= n2 ; sen eL = (n2/n1)

eL = arcsen (n2/n1)

La expresión anterior pone de manifiesto que sólo cuando n2 sea menor que n1 tiene sentido hablar ángulo límite, de lo contrario (n2 > n1) el cociente n2/n1 sería mayor que la unidad, con lo que eL no podría definirse, ya que el seno de un ángulo no puede ser mayor que uno.

Para ángulos de incidencias superiores al ángulo límite no hay refracción, sino sólo reflexión, y el fenómeno se conoce como reflexión interna total. También la reflexión total puede ser explicada a partir de la ley de Snell, Puesto que sen e2  1, la segunda ley de la refracción se podrá escribir en la forma:

o lo que es lo mismo:

pero n2/n1 es precisamente sen eL y, por tanto: sen e1  < sen eL, lo que supone que e2 <  eL

o en otros términos, la ley de Snell sólo se satisface, si n2 es mayor que n1, para ángulos de incidencia el menores o iguales al ángulo límite. Para ángulos de incidencia mayores, la refracción no es posible y se produce la reflexión interna total.

ESPEJOS

ESPEJOS PLANOS

Los espejos planos los utilizamos con mucha frecuencia. Si eres buen observador te habrás fijado en que la imagen producida por un espejo plano es VIRTUAL, ya que no la podemos proyectar sobre una pantalla, tiene el mismo tamaño que el objeto y se encuentra a la misma distancia del espejo que el objeto reflejado

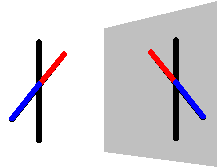
Habrás observado también que la parte derecha de la imagen corresponde a la parte izquierda del objeto y viceversa. Esto se llama inversión lateral.

Si la superficie del segundo medio es lisa, puede actuar como un espejo y producir una imagen reflejada (figura 2). En la figura 2, la fuente de luz es el objeto A; un punto de A emite rayos en todas las direcciones. Los dos rayos que inciden sobre el espejo en B y C, por ejemplo, se reflejan como rayos BD y CE. Para un observador situado delante del espejo, esos rayos parecen venir del punto F que está detrás del espejo. De las leyes de reflexión se deduce que CF y BF forman el mismo ángulo con la superficie del espejo que AC y AB. En este caso, en el que el espejo es plano, la imagen del objeto parece situada detrás del espejo y separada de él por la misma distancia que hay entre éste y el objeto que está delante.

Si la superficie del segundo medio es rugosa, las normales a los distintos puntos de la superficie se encuentran en direcciones aleatorias. En ese caso, los rayos que se encuentren en el mismo plano al salir de una fuente puntual de luz tendrán un plano de incidencia, y por tanto de reflexión, aleatorio. Esto hace que se dispersen y no puedan formar una imagen

ESPEJOS ESFÉRICOS

Los espejos: Por definición, espejo es el nombre que recibe toda superficie o lamina de cristal azogado por la parte posterior, o de metal bruñido, para que se reflejen en ella los objetos. Por extensión se denomina “espejo” a toda superficie que produce reflexión de los objetos, por ej. : la superficie del agua.

Por lo tanto, y a partir de la definición que hemos establecido previamente, extendemos el concepto: un espejo esférico esta formado por una superficie pulida correspondiente a un casquete esférico.

Los espejos esféricos pueden clasificarse en cóncavos o convexos; son cóncavos, aquellos que tienen pulimentada la superficie interior y son convexos los que tienen pulimentada la parte exterior

Hay dos clases de espejos esféricos, los cóncavos y los convexos.

El centro de curvatura (O) es el centro de la esfera a la que pertenece el casquete. Cualquier rayo que pase por este punto se reflejará sin cambiar de dirección.El centro del casquete esférico (C) se denomina centro de figura.La línea azul, que pasa por los dos puntos anteriones se denomina eje óptico.

El foco (F) es el punto en el que se concentran los rayos reflejados, para el caso de los espejos cóncavos, o sus prolongaciones si se trata de espejos convexos. Llamamos distancia focal de un espejo a la distancia entre los puntos F y C.

Elementos de los espejos esféricos:

Centro de curvatura: Es el centro de la esfera a la que pertenece el casquete.

Radio de curvatura: Es el radio de la esfera a la cual pertenece el espejo.

Vértice del espejo: Es el polo del casquete esférico al que pertenece el espejo.

Eje principal: Es la recta que pasa por el vértice y el centro de curvatura

Eje secundario: Cada una de las rectas que pasa por el centro de curvatura.

Abertura (o ángulo) del espejo: Es el ángulo formado por los ejes secundarios que pasan por el borde del espejo.

En los espejos esféricos se verifican las mismas leyes de reflexión que en los espejos planos. De hecho, se considera que el punto de incidencia del rayo pertenece al plano tangente al espejo esférico, en ese mismo punto.

La trayectoria de los rayos y los focos:

En los espejos esféricos cóncavos, se cumple que:

* Todos los rayos paralelos al eje principal se reflejan pasando por el foco (ubicado sobre el eje principal).

* Cualquier rayo que pase por el foco principal se refleja paralelo al eje principal.

* Todo rayo que pase por el centro de curvatura, se refleja sobre sí mismo. Esto se explica fácilmente en forma geométrica, ya que, si pasa por el centro de curvatura, es un radio y, todo radio es perpendicular a la recta tangente a la circunferencia en el punto donde ese radio corta a la circunferencia.

* Puede demostrarse geométricamente que el foco principal de un espejo esférico es el punto medio del radio de curvatura. Dada la relación entre lo anterior y la distancia focal, podemos también afirmar -y demostrar- que la distancia focal es igual a la mitad del radio de curvatura.

Hasta aquí, hemos hablado de los espejos esféricos cóncavos, ocupémonos ahora de los convexos:

En estos, también se cumplen las leyes de la reflexión ya conocidas y analizadas, pero debemos hacer la aclaración de que:

“el foco principal de un espejo esférico convexo, es virtual”, por lo tanto, la distancia focal de un espejo convexo es negativa.

Puede verificarse fácilmente que la trayectoria de los rayos en los casos de espejos esféricos convexos, es similar a la trayectoria en los espejos cóncavos, pero... como el foco es virtual, decimos:

* Cualquier rayo paralelo al eje principal, en un espejo convexo, se refleja de manera tal que su prolongación pasa por el foco.

* Todo rayo que incidiendo sobre un espejo convexo tiende a pasar por el foco se refleja en forma paralela al eje principal.

* Todo rayo que incide en dirección al centro del espejo, se refleja sobre sí mismo.

La imagen que surge en un espejo esférico convexo, es virtual, de igual sentido y menor que el objeto reflejado.

Los espejos “curvos”
Estas son algunas de las utilidades de estos espejos que hemos analizado:
* El dentista, el otorrinolaringólogo, etc. utilizan espejos esféricos cóncavos que tienden a concentrar los rayos luminosos en el lugar que desean observar en detalle.

* En el caso de los automóviles, la parte “pulida” de los faros son también espejos cóncavos.

* Los espejos retrovisores de los autos son de tipo convexo y, por lo tanto, forman una imagen virtual visible para el conductor.

Formacion de imagenes

Espejos concavos:

LENTES

Las lentes son medios transparentes limitados por dos superficies, siendo curva al menos una de ellas.

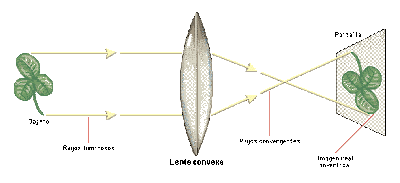
Lente convexa. Una lente convexa es más gruesa en el centro que en los extremos. La luz que atraviesa una lente convexa se desvía hacia dentro (converge). Esto hace que se forme una imagen del objeto en una pantalla situada al otro lado de la lente. La imagen está enfocada si la pantalla se coloca a una distancia determinada, que depende de la distancia del objeto y del foco de la lente. La lente del ojo humano es convexa, y además puede cambiar de forma para enfocar objetos a distintas distancias. La lente se hace más gruesa al mirar objetos cercanos y más delgada al mirar objetos lejanos. A veces, los músculos del ojo no pueden enfocar la luz sobre la retina, la pantalla del globo ocular. Si la imagen de los objetos cercanos se forma detrás de la retina, se dice que existe hipermetropía.

Lente cóncava. Las lentes cóncavas están curvadas hacia dentro. La luz que atraviesa una lente cóncava se desvía hacia fuera (diverge). A diferencia de las lentes convexas, que producen imágenes reales, las cóncavas sólo producen imágenes virtuales, es decir, imágenes de las que parecen proceder los rayos de luz. En este caso es una imagen más pequeña situada delante del objeto (el trébol). En las gafas o anteojos para miopes, las lentes cóncavas hacen que los ojos formen una imagen nítida en la retina y no delante de ella.

Las lentes con superficies de radios de curvatura pequeños tienen distancias focales cortas. Una lente con dos superficies convexas siempre refractará los rayos paralelos al eje óptico de forma que converjan en un foco situado en el lado de la lente opuesto al objeto. Una superficie de lente cóncava desvía los rayos incidentes paralelos al eje de forma divergente; a no ser que la segunda superficie sea convexa y tenga una curvatura mayor que la primera, los rayos divergen al salir de la lente, y parecen provenir de un punto situado en el mismo lado de la lente que el objeto. Estas lentes sólo forman imágenes virtuales, reducidas y no invertidas.

Si la distancia del objeto es mayor que la distancia focal, una lente convergente forma una imagen real e invertida. Si el objeto está lo bastante alejado, la imagen será más pequeña que el objeto. Si la distancia del objeto es menor que la distancia focal de la lente, la imagen será virtual, mayor que el objeto y no invertida. En ese caso, el observador estará utilizando la lente como una lupa o microscopio simple. El ángulo que forma en el ojo esta imagen virtual aumentada (es decir, su dimensión angular aparente) es mayor que el ángulo que formaría el objeto si se encontrara a la distancia normal de visión. La relación de estos dos ángulos es la potencia de aumento de la lente. Una lente con una distancia focal más corta crearía una imagen virtual que formaría un ángulo mayor, por lo que su potencia de aumento sería mayor. La potencia de aumento de un sistema óptico indica cuánto parece acercar el objeto al ojo,y es diferente del aumento lateral de una cámara o telescopio, por ejemplo, donde la relación entre las dimensiones reales de la imagen real y las del objeto aumenta según aumenta la distancia focal.

La cantidad de luz que puede admitir una lente aumenta con su diámetro. Como la superficie que ocupa una imagen es proporcional al cuadrado de la distancia focal de la lente, la intensidad luminosa de la superficie de la imagen es directamente proporcional al diámetro de la lente e inversamente proporcional al cuadrado de la distancia focal. Por ejemplo, la imagen producida por una lente de 3 cm de diámetro y una distancia focal de 20 cm sería cuatro veces menos luminosa que la formada por una lente del mismo diámetro con una distancia focal de10 cm. La relación entre la distancia focal y el diámetro efectivo de una lente es su relación focal, llamada también número f. Su inversa se conoce como abertura relativa. Dos lentes con la misma abertura relativa tienen la misma luminosidad, independientemente de sus diámetros y distancias focales.

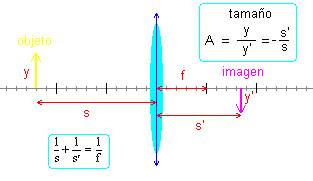
Tipo de lentes

Existen lentes convergentes y divergentes:

Tipos de lentes convergentes

Las lentes convergentes son más gruesas por el centro que por el borde, y concentran (hacen converger) en un punto los rayos de luz que las atraviesan. A este punto se le llama foco (F) y la separación entre él y la lente se conoce como distancia focal (f).

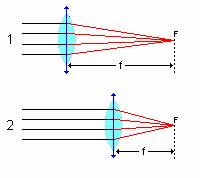
Observa que la lente 2 tiene menor distancia focal que la 1. Decimos, entonces, que la lente 2 tiene mayor potencia que la 1.

La potencia de una lente es la inversa de su distancia focal y se mide en dioptrías si la distancia focal la medimos en metros.

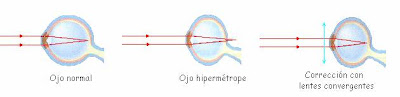
Las lentes convergentes se utilizan en muchos instrumentos ópticos y también para la corrección de la hipermetropía. Las personas hipermétropes no ven bien de cerca y tienen que alejarse los objetos. Una posible causa de la hipermetropía es el achatamiento anteroposterior del ojo que supone que las imágenes se formarían con nitidez por detrás de la retina.

Tipos de lentes divergentes

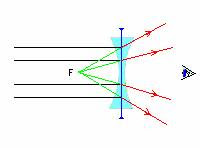
Si las lentes son más gruesas por los bordes que por el centro, hacen diverger (separan) los rayos de luz que pasan por ellas, por lo que se conocen como lentes divergentes.

Si miramos por una lente divergente da la sensación de que los rayos proceden del punto F. A éste punto se le llama foco virtual.

En las lentes divergentes la distancia focal se considera negativa.

La miopía puede deberse a una deformación del ojo consistente en un alargamiento anteroposterior que hace que las imágenes se formen con nitidez antes de alcanzar la retina. Los miopes no ven bien de lejos y tienden a acercarse demasiado a los objetos. Las lentes divergentes sirven para corregir este defecto.

Reglas de construcción de imágenes en las lentes.

Las trayectorias de los infinitos rayos que salen de un objeto están definidas por estas reglas:

Todo rayo que marcha paralelo al eje óptico antes de entrar en la lente, pasa, al salir de ella, por el foco imagen, F' .

Todo rayo que pasa por el foco objeto, F, llega a lente y se refracta en ella, emergiendo paralelo al eje óptico.

Todo rayo que pasa por el centro óptico (que es el centro geométrico de la lente) no sufre desviación.

Para localizar el punto imagen que de un objeto da una lente, debemos construir por lo menos la trayectoria de dos de los rayos más arriba mencionados. En el punto de cruce se forma el punto imagen:

Casos de formación de la imagen según la posición del objeto

 
Lentes convergentes

Formación de imágenes:

Si tomas una lente convergente y la mueves acercándola y alejándola de un folio blanco que sostienes con la otra mano, comprobarás que para una cierta distancia se forma una imagen invertida y más pequeña de los objetos que se encuentran alejados de la lente. Cuando es posible proyectar la imagen formada decimos que se trata de una imagen real, y si no la podemos proyectar la denominamos imagen virtual.

De cada uno de los puntos del objeto salen miles de rayos que llevan la información del objeto y se concentran en un punto donde se forma su imagen.

Las lentes convergentes, para objetos alejados, forman imágenes reales, invertidas y de menor tamaño que los objetos

En los gráficos que siguen el objeto se dibuja en negro. Si la imagen es real se ve de color azul y si es virtual en verde.

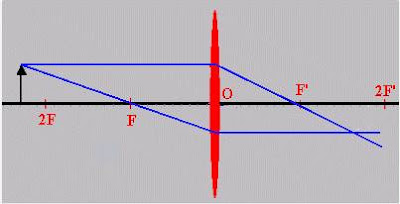
1.- Si el objeto está situado entre 2F y el infinito (menos infinito), la imagen estará entre F' y 2F' y será invertida, real y más pequeña.

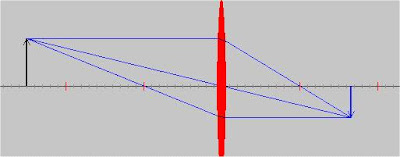
2.- Si el objeto está situado en 2f, la imagen estará en 2 F', y será de igual tamaño, invertida y real.

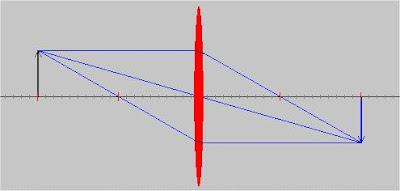
3.- Si el objeto está situado entre 2F y F, la imagen estará situada más allá de 2 F' y será mayor, invertida y real.

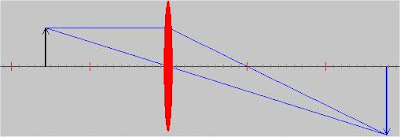
4.- Si el objeto está situado en F la imagen no se forma (se formaría en el infinito)

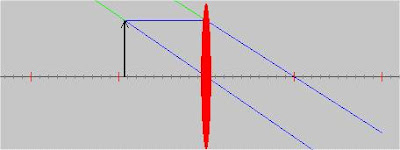
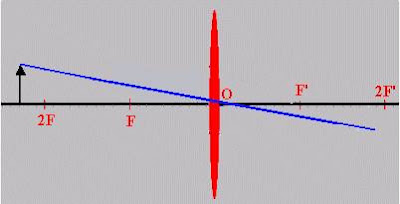
5.- Si el objeto está situado entre F y la lente, la imagen estará entre F y el infinito y será virtual (la forman las prolongaciones de los rayos), mayor y derecha.

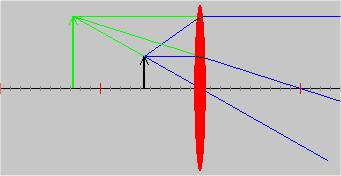
Lentes divergentes

Sea cual sea la posición del objeto frente a la lente la imagen siempre será virtual, menor y derecha.

INSTRUMENTOS DE ÓPTICA

Lupa

Una lupa es una lente convexa grande empleada para examinar objetos pequeños. La lente desvía la luz incidente de modo que se forma una imagen virtual ampliada del objeto (en este caso un hongo) por detrás del mismo. La imagen se llama virtual porque los rayos que parecen venir de ella no pasan realmente por ella. Una imagen virtual no se puede proyectar en una pantalla.

También llamada microscopio simple, esta formado por una lente convergente. Cuando el objeto se coloca entre el foco y la lente se forma una imagen derecha, virtual agrandada del mismo lado del objeto y entre el centro de curvatura y el infinito.

Microscopio compuesto

Un microscopio compuesto es un microscopio óptico que tiene más de un lente. Los microscopios compuestos se utilizan especialmente para examinar objetos transparentes o cortados en láminas tan finas que se transparentan. Se emplea para aumentar o ampliar las imágenes de objetos y organismos no visibles a simple vista.

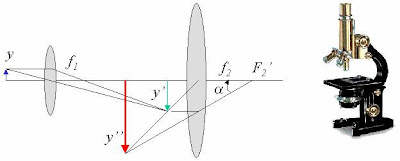
Comprende dos sistemas de lentes el ocular de distancia focal larga y el objetivo de distancia focal corta. La imagen que forma el objetivo es real y se ubica entre la lente y el foco del ocular, De esta forma será tratada como una lupa, observándose una imagen virtual muy agrandada.

Anteojo astronómico

En el anteojo astronómico cuando el objeto se encuentra entre el centro de curvatura y el infinito, la imagen que se forma es virtual e invertida

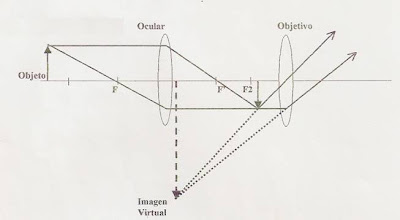
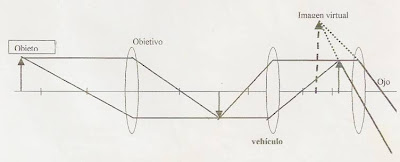
Anteojo Terrestre

El anteojo terrestre difiere del astronómico por que tiene una tercera lente intercalada, llamada vehículo que endereza la imagen.

Cámara fotográfica

Consta básicamente de una cámara oscura provista de una lente convergente u objetivo, formando una imagen mas pequeña real e invertida sobre la película.

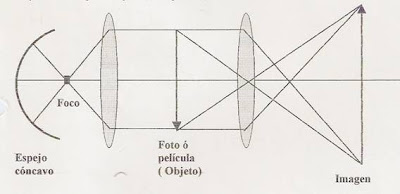
Aparato de Proyección

Se compone básicamente de un sistema de iluminación compuesto por un foco luminoso , un espejo cóncavo (reflector) y una lente convergente que actúa como condensador y de un sistema de proyección compuesto por una lente convergente y una pantalla donde se formará una imagen real, invertida y de mayor tamaño que el objeto (foto, película).

 

https://www.natureduca.com/fis_luzyop_propaluz04.ph
https://cienciasnaturales-fisica.blogspot.com/2007/03/fsica-ii-varios.html
https://web.educastur.princast.es/proyectos/fisquiweb/Apuntes/Apuntes2Fis/OpticaGeometrica.pdf